
Lecture notes: Introducing iteration plans
1. Goals and plans
There are typical problems or tasks for which there exist paradigmatic solutions. Expert programmers easily identify typical sub-problems in a problem and know their paradigmatic solutions. It is not a question of learning a set of “techniques” to apply blindly, but rather to understand the logic behind it and learn to think that way, if one wants to become an expert programmer.
We will use the terms:
- goal: each sub-task that must be dealt with in the solution of a problem
- plan: the paradigmatic solution for a specific goal.
Examples of goals:
- compute the sum of a series of numbers
- verify if a float can be considered “uguale” (close enough) to a given value
Examples of corresponding plans:
sum :=0for _,n := range series {sum += m}math.Abs(x - val) < EPSILON
To illustrate the concepts of goal and plan let us consider the problem of computing the average of a sequence of numbers terminated by 9999.
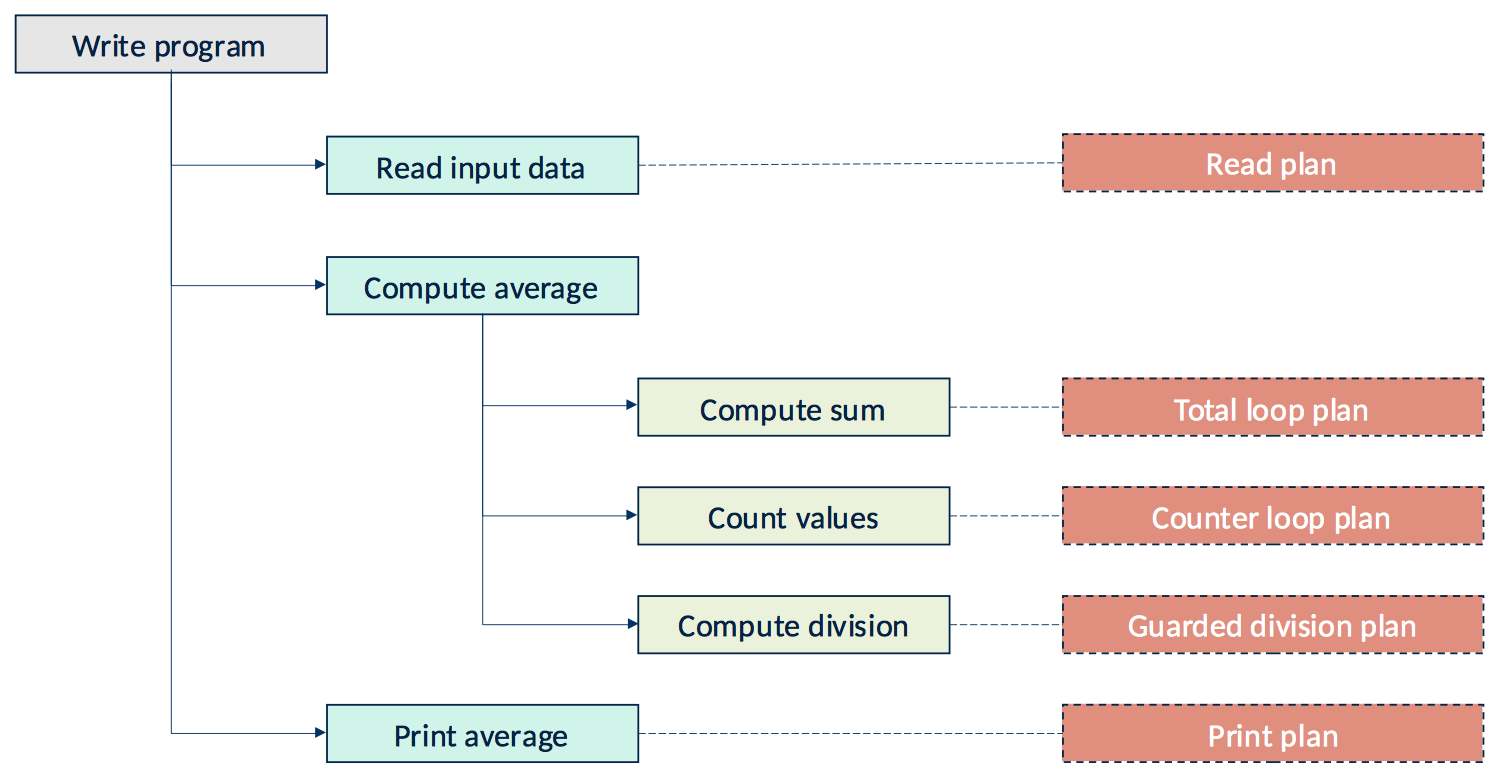
As shown in the figure, we can identify three main goals:
- reading of the input numbers
- computation of the average, which in turn can be decomposed into three sub-goals:
- computation of the sum of the input numbers (the terminating value 9999 excluded)
- count of the input numbers (the terminating value 9999 excluded)
- division between the sum and the count of the input numbers, checking that the count is different from zero
- printing of the output
An expert programmer will immediately identify the listed goals and will propose a typical solution with:
- a plan for reading the numbers
- a plan for summing the read numbers
- a plan for counting the read numbers
- a plan for dividing sum by count, checking not to do a division by 0.
- a plan for printing the resulting average.
We will also deal with aggregate tasks and plan composition in a program in a subsequent section.
2. Iteration goals and plans: typical problems
We will now present typical problems whose solution requires a plan based on iteration and will show the corresponding plans.
Note: in the following examples the variables that have a special role in the plan have a comment highlighting this aspect.
We will write more on this aspect in the following section.
- Goal: repetition, that is repeating an action (or a sequence of actions) n times.
Plan:
for i:=1; i<=n; i++ {
action
}Example: Print a star (’’) n* times. In the repetition plan the block of instructions in the loop defines the action (or sequence of actions) to be carried out a certain number of times.
Sometimes the loop index is used in the instructions too in order to have parametric actions. For example:
for i:=1; i<=n; i++ {
fmt.Println(i*i)
}- Goal: computation of a total amount
Plan:
total :=0 // var with a fundamental role
for i:=1; i<=n; i++ {
total += new_value
}Example: Sum or multiply the numbers in a series. But also concatenate a series of strings or of characters into a single string. See also Snippets 2, 4, and 6.
In particular, note that in the total loop plan there is always a variable (in Snippet 2 product and in Snippets 4 and 6 sum) which is suitably initialized before the loop and then updated at every iteration.
- Goal: counting Plan:
count := 0 // var with a fundamental role
for condition {
count++
}Example: Count the number of iterations needed to reach a goal/result.
The counting loop plan is very similar to the total loop plan. It too has a variable which is suitably initialized before the loop and then updated at every iteration, with the difference that in this case it has the role of counter, incremented by 1 at each iteration.
- Goal: identification of the first (possible) occurrence of an item and/or its position (i.e. linear search)
Plan:
found := false // var with a fundamental role
//or, in alternative
//pos := - 1 // var with a fundamental role
for i:=1; i<=n; i++ {
if condition on item i {
found = true
//or, in alternative
//pos = i
break
}
}Example.: Find the first even number in a sequence.
The linear search loop plan must handle both the case the searched value is present and the case it is not. Therefore, in case also the searched value’s position in the sequence must be determined, a variable for the position is used initializing it at a value of a non valid position, typically -1, and updating it if and when the value is found. Otherwise, and especially if the position is not relevant, a boolean variable is used with the role of one-way flag initialized to false and turned to true if and when the value is found.
- Goal: search of an extreme value (e.g. maximum or minimum).
Plan:
//initialization of extreme with the first element
// of the sequence or the minimum/maximum possible
extreme := init_value // var with a fundamental role
for there is a next element {
if next < extreme { // or >
extreme = next
}
}Example.: Find the maximum or the minimum in a sequence of values. See also Snippets 1, 3, and 7.
In particular note that in the extreme loop plan there always is a variable (maxM in Snippet 1, lastDayOfRain in Snippet 3, and min in Snippet 7) that is initialized before the loop with the first value of the sequence or with a bound of the values’ domain (e.g. 0 or math.MinInt64 or math.MaxInt64). In the loop it is then updated every time a value is found that is more extreme (for example greater or smaller) than the one stored in such variable.
- Goal: processing of adjacent values
Plan:
fmt.Scan(¤t)
for i:=1; i<=n; i++ {
previous = current // vars with a fundamental role
fmt.Scan(¤t)
//here sometimes an if with a condition on current and previous {
action on current and previous //}
}Example.: Analyze the trend of numeric values in a sequence / process contiguous values. See also Snippets 5, 8, and 9. Note that in the adjacent values iteration plan two (or more, depending on how many adjacent values must be considered) variables (number[i] and number[i-1] in Snippets 5 and 8, previous and current in Snippet 9) scan the sequence “arm in arm”, assuming, at each iteration, the first the second one’s value and the second one the next value to be considered.
3. Variables’ roles
Considerations similar to the ones on iteration goals and plans can be done on variables. Besides the concept of variable as holder of a mutable value of a given type, it is in fact important to learn the specific use cases of variables in the solution of problems. We talk in this case of roles of variables. Consider, for example, the problem of computing the sum or the maximum of a sequence of numeric values: there are variables needed in the implementation of the program that play a fundamental role (sum, max).
In presenting the iteration plans we pointed out with a comment the variables that play a fundamental role and that therefore belong to the plan itself.
We will resume them here, associating them with the related plans:
| Role | Plan | Examples | Informal definition |
|---|---|---|---|
| Gatherer | Computation of a total amount | sum, total, new_string | It gathers the contribution of each value |
| Stepper | Counting/ Position in linear search | count, index | It takes a sequence of values that vary in a systematic and predictable way |
| One-way flag | Linear search | found, errorsOccurred | A bi-valued variable (often boolean) that can change value only once |
| Most-wanted holder | Search of an extreme value | max, min | It holds the best result obtained so far |
| Follower (also prev-curr) | Processing of adjacent values | previousValue and currentValue | Variable (the follower/prev) that is updated with the previous value of another variable (the followed/curr) |
As already pointed out in the description of iteration goals and plans:
- The total iteration plan will have a gatherer variable, initialized before the loop to a starting value (e.g. 0 for the sum, 1 for the product, "" for a string, but possibly also different values depending on the problem) and which is updated in the loop.
- Il counting loop plan will have a stepper variable, initialized before the loop to a suitable value (often 0 or 1, but the problem could require a different value) and which is updated in the loop.
- The linear search loop plan, for the search of the first occurrence, will have a one-way flag variable, initialized before the loop to a suitable value (naturally to
false, but the problem could require a different value instead) and which is updated only once in the loop, usually in anifstatement withbreak.
In case (also) the position is requested, one can do without the one-way flag variable and use a stepper variable that records the position and is initialized to a non-valid position (typically -1, but the problem might require a different value); in this case the variable holding the position also reveals if the value is not present. - The extreme loop plan will have a most-wanted holder variable, initialized before the loop to a suitable value (typically either the first value in the sequence or a bound of the values’ domain, e.g. 0 for a max on non negative values, but, as always, the problem might require a different value) and which is updated in the loop.
- The adjacent values iteration plan will have a followed variable, initialized before the loop and updated in the loop, and a follower variable updated in the loop before followed is updated.
